簡介
|
【簡介】
|
【圓錐曲線的類型】
|
【離心率】
|
【離心率對應圖形】
|
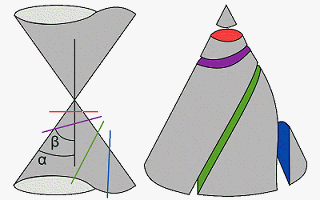
圓錐曲線(conic section),又稱為圓錐截痕、圓錐截面、二次曲線。為空間中以平面在不同角度平切圓錐(嚴格來為一個正圓錐面和一個平面完整相切)所得到的一些曲線。 圓錐曲線在約西元前200年時為古希臘的數學家阿波羅尼阿斯(Apollonius of Perga,前262年~前190年)發現與命名,並對其性質做系統性的研究。 |
|
|
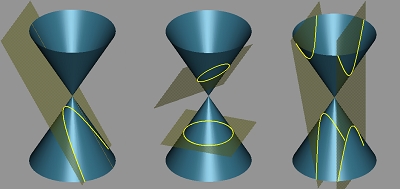
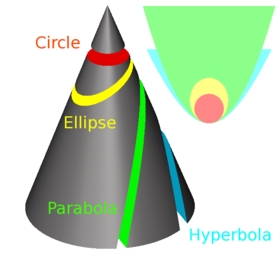
圓錐曲線中最常聽到的是『圓(Circle) 』和『橢圓(Ellipse) 』,這二個曲線出在圓錐和平面的相交截線是閉合曲線的時候。而圓是橢圓的特殊情況,圓產生在平面垂直於圓錐的軸線時。 如果平面平行於圓錐的母線(generator line)所截得之曲線稱之為『拋物線Parabola 』。 若平面與軸線的夾角小於軸線與母線的夾角,則這個圓錐曲線為『雙曲線(Hyperbola)』,這種情況平面將交二垂直對稱之直圓錐的兩段,而生成兩個分開的曲線。 |
|
|
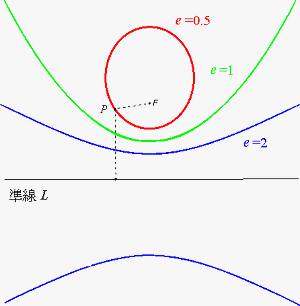
圓錐曲線存在的四種情況,可以合併歸納以『固定的一個點 `F`(焦點)、不包含 `F` 的一個直線` L`(準線),以及一個非負實數 `e` (離心率) 來定義』。離心率 `e` 定義為:『動點`P`到焦點`F`之距離,與動點`P`到準線` L` 的距離之比值』,亦即『`e = (d(P,F))/(d(P,L))`』。 平面上的動點`P`在不同離心率情況之下,其形成的軌跡圖形對映到不同的圓錐曲線。當` 0<e<1`可以得到橢圓。離心率` e = 1` 得到拋物線。離心率` e > 1` 得到雙曲線。 |
|
|
參考資料:維基百科。