橢圓的3D定義
|
圓柱切橢圓及內切球
在平面的截面與圓柱之間塞球進去,使球跟截面、圓柱皆相切。而這樣的球我們可以上下各塞進一個,且這兩球與截面的切點,便是橢圓的兩個焦點!
圓錐截橢圓及內切球
在平面的截面與圓錐之間塞球進去,使球與圓錐、截面皆相切。而這樣的球我們可以上下各塞進一個,且這兩球與截面的切點,便是橢圓的兩個焦點!
圓錐截橢圓與內嵌球證明
3D模擬
如圖
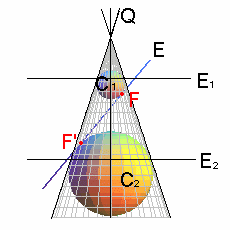
設 `E` 為不通過 `Q` 頂點的一平面,且其法向量與 `Q` 的中心軸之間的夾角小於 `90°-w` ,這時 `Q` 與 `E` 的交線 `T` 是一橢圓。在錐面內 `E` 的兩側各有一個球面同時與平面 `E` 及錐面相切,這兩球面與平面 `E` 的切點 `F` 與 `F'` 便是橢圓的焦點,又兩球面與錐面相切於兩圓 `C_1` 與 `C_2`,這兩圓分別落在兩水平面上。
如圖
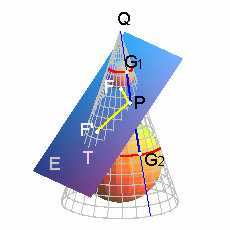
自 `T` 上任一點 `P` ,作 `P` 與錐面 `Q` 頂點的連線,分別交圓 `C_1` 與圓 `C_2` 於 `G_1` 與 `G_2` , 則有`bar(PF) = bar(PG_1)`,`bar(PF') = bar(PG_1)`,因此 `bar(PF) + bar(PF') = bar(PG_1) + bar(PG_2)= `定長,表示 `T` 上任一點 `P` 到 `F` 與 `F'` 兩定點的距離和是定數,故 `T` 為一橢圓!
如圖
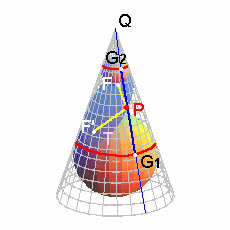
另一個角度觀看圓錐與平面的截痕,橢圓的曲線更清楚易見! |
|