拋物線的3D定義
|
3D實驗圖1
3D實驗圖2
圓錐內嵌球1
如圖
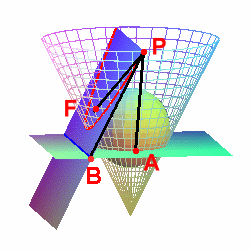
在平面與圓錐間放一球,使球與平面及圓錐相切,球與平面切於 `F` 點,`F` 點即為拋物線之焦點。此時,拋物線上的點 `P` 與 `F` 之距離即為點到球之切線長,`P` 到切圓的垂直距離 `bar(PA)` 是球的另一條切線,所以 `bar(PF)=bar(PA)` 。
如圖
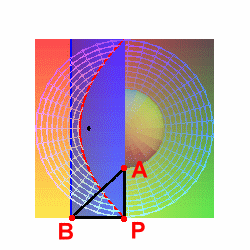
若可證明 `bar(PA) = bar(PB)`,即可證明拋物線所在的平面與切圓的平面,兩平面相交之直線即為拋物線準線。換個角度,從正上方俯看整個圖, `P` 、`A` 、`B` 三點投影在切圓平面上看似一等腰直角三角形,如果是的話,即可證明 `bar(PA)=bar(PB)`。 如圖
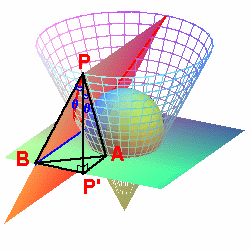
設圓錐的張角為`θ`,則 `∠PAP'= θ`,又拋物線所在的平面平行圓錐稜線,得`∠PBP'=θ`, 加上 `∠PP'A=∠PP'B=90°` , `bar(PP')=bar(PP')` , `ΔPP'A`全等於`ΔPP'B` (ASA性質),所以`bar(PA)=bar(PB)`,故得證,此兩平面所交之直線為拋物線之準線!
圓錐內嵌球2
如圖
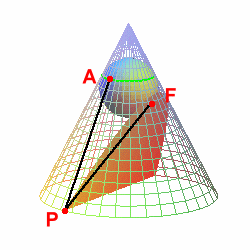
在平面與圓錐間放一球,使球與平面及圓錐相切,球與平面切於`F`點,`F`點即為拋物線之焦點。此時,拋物線上的點`P`與`F`之距離為點到球之切線長,`P`到切圓的垂直距離`bar(PA)` 是球的另一條切線,所以 `bar(PF)=bar(PA)`。 |
|